Görelilik popüler kültür ve yazında üzerine en çok konuşulan, en çok manipülasyon yapılan, kafa yorulan fizik olgularından birisidir. Bu yazı birbirine göre sabit hızla hareket eden gözlemcileri kapsayan özel görelilik üzerine az matematik az fizik bilen bünyeleri hedef alan küçük bir temrin yazısıdır.
İki gözlemci arasındaki ölçümlerin birbirleri ile nasıl ilişkilendirileceklerine dair temel kurallardan başka bir şey olmayan göreliliğin Einstein’ın muzip kişiliği sayesinde popülerliği oldukça yüksektir. Ancak görelilik fikri Einstein’dan yüz yıllar önce Galilei ile fiziğe dahil olmuştur. Kinematiği bize armağan eden Galilei hareketli nesnelerin birbirlerine göre bağıl hız ve konum ölçümleri üzerine de kafa yormuştu. Bugün birçok yerde kullandığımız ama Galilei ile anmadığımız o göreliliğin kurallarına kısaca bir göz atalım. Yalnız bunu yaparken sabit hızlardan bahsettiğimiz için dönme vs. gibi olguları dışlayacağımızdan kolaylık olması nedeniyle uzayımızı tek boyutlu olarak kabul edeceğiz. Daha sonra bunu üç boyuta genelleştirmek oldukça kolay olacaktır. Öyleyse başlayalım.
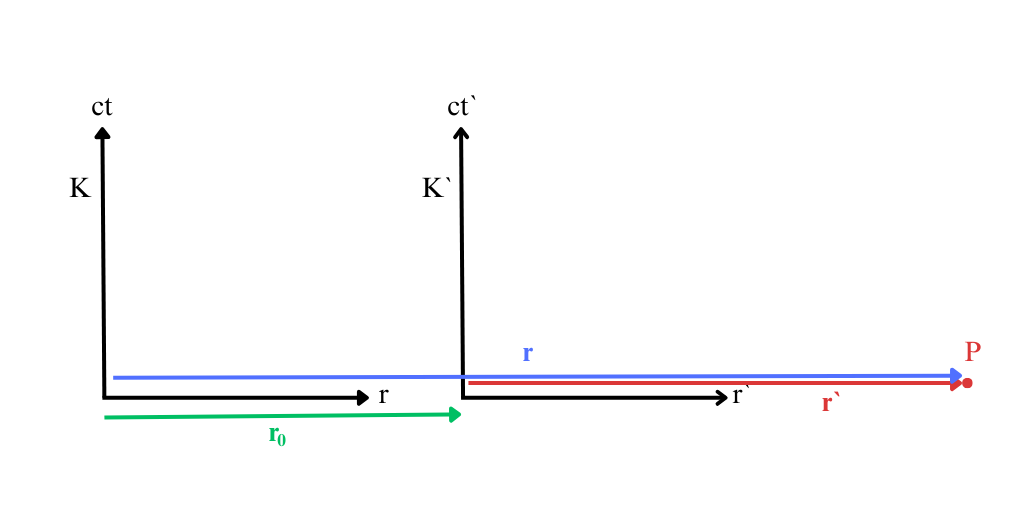
Şekil 1’deki iki gözlemciyi ele aldığımızda $K$ ile işaretlediğimiz gözlemci kendisinden $r$ kadar uzaktaki $P$ parçacığının hızını $v$ olarak ölçsün. $K$ gözlemcisine göre $u_0$ hızıyla hareket eden $K^\prime$ gözlemcisi ise kendisine göre $r^\prime$ uzaklıkta olan aynı $P$ parçacığının hızını $v^\prime$ olarak ölçecektir. Galilei göreliliğinin en temel özelliği iki gözlemci için saatlerin aynı hızda çalıştığıdır. Yani $K$ gözlemcisinin $t$ olarak ölçtüğü süre ile $K^\prime$ gözlemcisinin ölçtüğü $t^\prime$ süresi birbirine eşittir:
\begin{equation}
t=t^\prime\,.
\end{equation}
Peki uzunluk ölçümü arasındaki kural nasıl olmalıdır? Bunu belirlemek aslında kolaydır. Gelin tam ölçüme başladığımız anda $K$ ve $K^\prime$ gözlemcilerinin aynı noktada olduklarını varsayalım. $t$ kadar süre geçtiğinde aralrındaki mesafeye $r_0$ dersek, $K^\prime$ gözlemcisi $u_0$ hızıyla $K$ gözlemcisinden uzaklaştığına göre, $r_0$
\begin{equation}
r_0 = u_0 t
\end{equation}
kadar olacaktır. Bu da iki gözlemcinin $P$ parçacığın konum ölçümleri arasındaki farka eşit olmalıdır. Yani $r_0 = r-r^\prime$ olacaktır. Bu durumda $r$ ve $r^\prime$ arasındaki dönüşüm kuralı
\begin{equation}
r=r^\prime + u_0 t
\end{equation}
olmalıdır. Öyleyse Galilei göreliliğinin dönüşüm kurallarını bir kez yazalım:
\begin{align}
t &= t^\prime, \\
r &= r^\prime + u_0 t .
\end{align}
Bu iki gözlemcinin ölçtükleri hızlar arasındaki ilişki ise $r$’nin zamana göre türevinden başka bir şey olmayacağı için
\begin{align}
v&=v^\prime + u_0 \\
\frac{d r}{dt} &= \frac{d r^\prime}{dt} +u_0
\end{align}
şeklinde bulunur. Bunun bir kez daha zamana göre türevi alındığında ivmeler arasındaki ilişki
\begin{align}
a&=a^\prime \\
\frac{d^2 r}{dt^2} &= \frac{d^2 r^\prime}{dt^2}
\end{align}
şeklinde bulunmuş olur. Görüleceği üzere $u_0$’ın sabit olması nedeniyle iki ivme birbirine eşit çıkmıştır. Buradan da şu birkaç sonucu çıkarabiliriz:
1) Galilei dönüşümleri Newton hareket denklemlerini değiştirmeyen koordinat dönüşümleridir. Birbirlerine göre bu kuralla dönüşen, yani birbirine göre sabit hızla hareket eden gözlemciler “eylemsiz referans sistemleri” olarak adlandırılırlar.
2) Galilei göreliliği 19. YY ortasına kadar klasik fiziğin uyduğu görelilik kuralıdır.
Buna göre dinamik denklem ve enerji eşitlikleri şöyledir:
\begin{equation}
F = m \qquad \text{ve}\qquad E= \frac{1}{2} m v^2 + V(r)
\end{equation}
Elektromanyetik teorinin 1865’ten itibaren olgun bir teori haline gelmesi üzerine bu kuramın uyduğu görelilik kurallarının bulunması gerekiyordu. Bu kurallar Lorentz tarafından bulunmuştu. Yukarıdaki $K$ ve $K^\prime$ gözlemcilerini hatırlarsak bu gözlemcilere göre Lorentz dönüşüm kuralları
\begin{align}
t^\prime &= \gamma \left( t – \frac{u_0 r}{c^2}\right) \\
r^\prime &= \gamma \left(r-u_0 t\right)
\end{align}
biçiminde olacaktır. Burada $\gamma$ $u_0$’a bağlı bir parametredir ve
\begin{equation}
\gamma = \sqrt{1+\frac{u_0^2}{c^2}}
\end{equation}
şeklinde ifade edilir. $c$ ise çok iyi bilindiği üzere ışık hızıdır. Lorentz bu dönüşümleri elektromanyetizmanın temel alan denklemleri olan Maxwell denklemlerinin ve Maxwell denklemlerinden türetilen elektromanyetik dalga denkleminin değişmezliği üzerinden bulmuştur.
Lorentz’in bu dönüşümleri bulması Einstein’a altı pas içinde boş kaleye yuvarlanacak bir gollük pastan başka bir şey olmayacaktır. Einstein’ın fizik içgüdüleri bu kuralların sadece ışık için değil tüm fiziksel sistemler için geçerli olduğunu söylemiş ve Özel Görelilik Kuramı buradan kökünü almıştır.
Peki özel görelilikteki dinamik denklem ve enerji ifadesi nasıldır? Şöyle1 Kuvvet ifadesi tek bir uzay boyutu olduğu durumda iki gözlemci tarafından da aynıdır. Ancak iki veya daha fazla uzay boyutu olduğunda bu ifade değişir.:
\begin{equation}
F^\prime = F=\gamma^3 m a\qquad \text{ve}\qquad E^2 = p^2 c^2 + m^2 c^4
\end{equation}
Burada $p=\gamma m v$ olup parçacığın momentumudur ($\gamma= \sqrt{1+\frac{v^2}{c^2}}$). Bir de 4-momentumu vardır ki onu $P=\left(\frac{E}{c},p\right)$ biçiminde ifade etmeyi tercih edeceğim ancak şu an için tartışmamızda yeri yok.
Şimdi burada fiziğin en önemli epistemolojik özelliğine değinmek zorundayız. Fizik içererek aşan bir ilerlemeye yani yeni gelen bilginin eski bilgiyi içermekle beraber ekstra bilgi vermesi üzerine kuruludur. Kısacası fiziğin epistemolojisi diyalektik bir ilerleme gösterir. Bunu görelilik kapsamında ispatlamak mümkündür. Bunun için yukarıdaki ifadelerdeki $u_0$ ve $v$ hızlarının ışık hızından çok çok küçük olduğu limit durumuna bakmamız gerekir ($v/c\ll 1$, $u_0/c\ll 1$ veya $v/c \simeq 0$, $u_0/c \simeq 0$). Bu limit durumunda $\gamma \simeq 1 +\frac{1}{2} \frac{v^2}{c^2} \simeq 1$ olur.
Dinamik denklem bir boyutlu uzay için zaten gözlemciden bağımsızdır. Ancak enerji ifadesi bize güzel bir fikir verir. Gelin bakalım:
\begin{align}
E &=\sqrt{p^2 c^2 + m^2 c^4} \\
&= m c^2 \sqrt{1+\frac{p^2}{m^2 c^2}} \\
&\simeq mc^2 \left(1+\frac{p^2}{2 m^2 c^2}\right)\\
&= \frac{p^2}{2 m} +m c^2.
\end{align}
Son olarak $p= \gamma m v \simeq m v$ bilgisini de kullanırsak
\begin{equation}
E= \frac{1}{2} m v^2 +m c^2.
\end{equation}
elde ederiz. Kinetik enerji teriminin düşük hızlarda Newton mekaniğindeki kinetik enerji ifadesiyle aynı olduğunu görürüz.
Yazı göreliliğin bir özeti olması ve amacıyla yazıldığı için bu noktada kesebiliriz. Aksi durumda bir elektromanyetik teori kitabına bir bölüm yazmış olurduk. O nedenle bu noktada keselim.


