Şimdi bazı hayal dünyasında yaşayan zevat diyor ki: Dünyayı matkapla tenis topu deler gibi bir noktadan delip tam karşı noktadan çıksak sonra da bu kuyuya atlasak başımıza ne iş gelir? Gelin gundiler açıklıyoruz.
Öncelikle biz Dünya’yı bir küre olarak var sayacağız. Halbuki Dünya yüzeyi uzaktan düz gibi duruyor olsa da bildiğiniz üzere Everest ile Mariana çukurunun rakım farkı 17 km olan çarpık çurpuk bir nesne. Ayrıca küre de değil. Hiçbir boka benzetilemediği için şekline özel bir geometrik kavram icat edilmiş: Geoid . Öyle çok düz bir yer değil ama bu 17 km’lik “devasa” fark, 6378 km olan Dünya yarıçapıyla kıyaslanamaz. Bunu kıyaslayan kişi, fille karıncayı da ebat olarak kıyaslayabilecek tıynette bir ölçek yoksunudur. Fantezi bu ya farzedelim ki teknolojimiz imkân verdi ve Dünya’yı deniz seviyesinde ve denizden yeteri kadar uzaktaki bir kara parçasından delmeye başlayıp yine deniz seviyesinde ve denizden yeteri kadar uzakta bir noktadan çıktık. Delikten çıkacak gazlar bir yana başımıza gelecek diğer şey çukurun da atmosferi yutacak olmasıdır1 Bu yaşandığında kahramanımızın başına ne geleceğini hesaplamak bir başka yazının konusu olacak.. Ayrıca çıkan gazlarla dünya yaşanmaz falan olur ama gelin biz yine iyimser olalım ve atmosfer yerinde dursun hiç o deliğe kaçmasın; çekirdek, magma falan çok sıcak olmasın yani şöyle anlatayım ben siz gevşek ruhlulara: haziran ayında İzmir’de sahilde hafif meltem eserkenki sıcaklıkta olsa bizim deliğin içi.
İki şeyden yırttık: hava sürtünmesi ve magmanın ve çekirdeğin sıcaklığı ile kebap olmaktan. Üstelik atmosferimiz de bize kaldı. Ama cefakar halkımızın dertlerini anlattığı tarhana kokulu türkülerimizin dediği gibi bu Dünya denen gezegen bozuntusu fırıldaktır. Fırıl fırıl kendi ekseni etrafında döner. Dolayısıyla coriolis kuvveti vardır. O kuvvattır ki o deliğe atlayan yiğidi deliğin çevresine çarpa çarpa parçalar alim Allah. O nedenle problemimizde Dünya kendi ekseninde dönmesin veya biz deliği tam olarak dünyanın kendi etrafında dönme ekseninden açalım diye varsayalım ki atlayan maceraperest tek parça kalsın.
Bu noktada kuyuya atlayacak olan süpermanyağa etkiyecek ivmenin matematiksel ifadesini gelin Newton Reyiz’in o ünlü kütle çekim kuvveti ifadesinden çıkaralım. Üniversite birinci sınıf fizik öğrencisi eblehliğine sahip olmadığımız için bahsettiğimiz denklemin vektörel olduğunu, yani doğrultu ve yön bilgisine de sahip olduğunu unutmamalıyız. Ancak bundan yırtmamızı da sağlayacak bir imkâna sahibiz. Problemimizdeki kuyunun yarıçapı Dünya’nın yarıçapı yanında yaklaşık on milyonda bir katı kadar küçük olacağı için problemimizi bir boyutlu varsayabiliriz. Bu da bize vektörlerle değil de skaler niceliklerle çalışma imkânı veriyor. Bu durumda yön bilgisini de $+$ ve $-$ işaretleriyle verebiliriz. Öyleyse sözü matematiğe bırakabiliriz artık, yani Newton’un ikinci yasasını yazalım: \[ m a = – G_N \frac{M m}{r^2}. \] Bu denklemde eşitliğin her iki tarafında bizim kahramanımızın kütlesi olan $m$ olduğu için kendisinden kurtulabilir ve ivme ifadesini elde edebiliriz: \[ a = – G_N \frac{M}{r^2}. \] Yani bu demektir ki yerçekimi altında hareket eden nesnenin hareketi sıkletinden bağımsızmış2 Genel göreliliğin ilhamlarından birisi bu ayrıntıdadır. . İlkokuldayken bize “1 kg pamuk mu yoksa 1 kg demir mi daha ağırdır?” diye soru soran öğretmenlerimizin kulaklarını bu noktada çınlatabiliriz3 Yeteri kadar sövdükten sonra okumaya devam ediniz. .
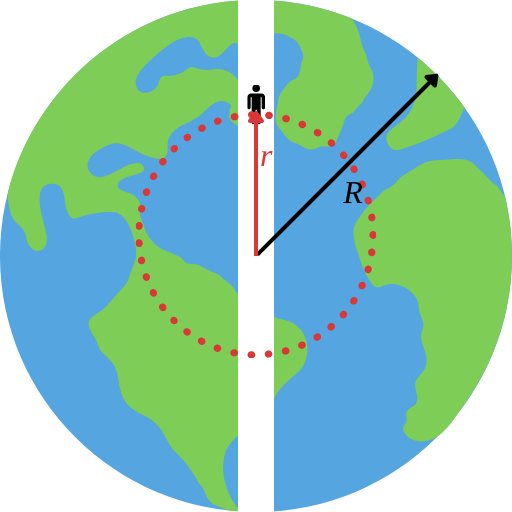
Bu denklemde yine önemli birkaç incelik vardır. Ama öncesinde size denklemdeki her bir niceliği takdim edeyim. Denklemde $a$ deliğe atlayan arkadaşın ivmesidir. $G_N$ Newton’un evrensel kütle çekim sabitidir ve değeri $6.674 \times 10^{−11} m^3 kg^{−1} s^{−2}$’dir. $r$ ise kuyuya atlayan arkadaşın Dünya’nın merkezine olan uzaklığıdır. $M$ ise bu $r$ yarıçaplı küre yüzeyi içinde kalan Dünya kütlesidir. Biz bu $M$ kütlesini Dünya’nın merkezinde yoğunlaşmış varsayarız. Bunu yapmaya hakkımızın olduğunu bizlere Gauß4Almanca bilmeyenler için ß = ss bilgisini de verelim. ünlü diverjans teoremiyle ispatlamıştır. Peki bizim elemanın merkeze olan uzaklığı olan $r$ hareketi boyunca değişecek. Dolayısıyla $M$ de $r$ ile beraber değişecek yani $M$ $r$’nin $M(r)$ gibi bir fonksiyonu olacak. Peki biz bu $M(r)$ fonksiyonunu nasıl bulacağız?
$M(r)$ fonksiyonunu bulmak için Dünya’nın morfolojik yapısına inceden bir eğilmek gerekir. Dünya’nın yüzeyinde bizim için oldukça kalın gibi dursa Dünya’nın yarıçapı ile kıyaslanınca oldukça ince bir kabuk tabakası vardır. Bu kabuğun içinde Dünya yarıçapının yarısından biraz az kalınlıkta bir manto ve onun içinde de iç ve dış çekirdek bulunur. Bu katmanların herbiri de farklı yoğunluktadır. Öyleyse yoğunluk da $\rho(r)$ şeklinde merkezden olan uzaklığın bir fonksiyonu olmalıdır. Bu durumda $r$ yarıçaplı küre yüzeyinin içinde kalan kütle şöyle hesaplanır: \[ M(r)= 4 \pi \int_0^r \rho(r^\prime) {r^\prime}^2 d r^\prime . \] Burada integral sınırı olan r ile integral değişkeni karışmasın diye integral değişkenini $r^\prime$ olarak aldım. Peki biz bu $\rho(r)$ yoğunluk fonksiyonunu nereden bulacağız? Bulmayacağız. Biz kolaylık olsun diye dünyanın bütün katmanların aynı yoğunlukta ve sabit olduğunu varsayabiliriz. Yani Dünya’nın ortalama yoğunluğunu $\rho_0$ gibi bir sabit alacağız. Bu durumda kütle fonksiyonu \begin{align}
M(r) =& 4\pi \rho_0 \int_0^r {r^\prime}^2 d r^\prime \\
=& \frac{4 \pi}{3} \rho_0 r^3
\end{align} olur. Şimdi bu ifade doğru olsa da pek kullanışlı değildir. Daha kullanışlı olması için $\rho_0$’ı Dünya’nın toplam kütlesi cisinden yazmamız gerekir. Eğer yukarıdaki integralde üst sınırı dünyanın yarıçapı R olarak alırsak \[ M_\oplus = \frac{4 \pi}{3} \rho_0 r^3 \] elde edilir. Burada $M_\oplus$ Dünya’nın toplam kütlesidir ve $5,97 x 10^{24}\, kg$ değerindedir. \[ \rho_0 = \frac{3 M_\oplus}{4 \pi R^3} \] yazabiliriz. Bu durumda $M(r)$ kütle fonksiyonu \begin{align}
M(r)=& \frac{4 \pi}{3} \frac{3 M_\oplus}{4 \pi R^3} r^3 \\
=& \frac{M_\oplus}{R^3} r^3
\end{align} biçiminde sade bir hâl alır. Şimdi bu kütle fonksiyonunu yukarıdaki ivme ifadesine yerleştirelim: \begin{align}
a =& – G_N \frac{M_\oplus}{R^3} r^3 \frac{1}{r^2} \\
=& – G_N \frac{M_\oplus}{R^3} r.
\end{align}
Artık hareket denklemimiz son halini aldı. Bu hareket denkleminde bir incelik daha vardır. O da eşitliğin sağ tarafındaki “$-$” işaretidir. Eğer bu “$-$” olmasa denklemin çözümleri hiperbolik olur ve kahramanımız delikten hızlanarak geçer ve uzaya doğru hızlanarak devam eder ve uzayda da hızlanmasını sürdürür. Bunun yanlış olacağını gözlemlerimiz ve buna dayanan sağduyumuz bize söyler. Yani denklemde o “$-$” işareti olmalı.
Sistemin hareket denklemini biliyorsak artık dinamiğini de biliyoruz demektir. Dinamik ise zamana göre değişimler, yani denklemlerde zaman türevlerinin olması demektir. İvme’nin tanımını kullanırsak hareket denklemini \[ \frac{d^2 r}{dt^2} = – G_N \frac{M_\oplus}{R^3} r \] şeklinde yazmak da mümkün olur. Bu denklemdeki $G_N$, $M_\oplus$ ve $R$ nicelikleri sabit olduğundan bunların hepsini $\omega_0^2$ gibi bir sabitle temsil etmek mümkün olur. Şimdi denklemi tekrar yazalım: \[ \frac{d^2 r}{dt^2} + \omega_0^2 r=0.\]
Artık tek yapmamız gereken bu denklemi çözmektir. Bu ikinci mertebeden sabit katsayılı lineer diferansiyel denklemleri çözmek kolaydır ama bunu da burada anlatarak bu yazıyı daha da okunmaz hale getirecek değiliz. Bu denklemin en genel çözümü şöyledir: \[r(t) = A cos(\omega_0 t) + B sin(\omega_0 t). \] Burada $A$ ve $B$ iki sabit katsayıdır ve problemin başlangıç koşullarına göre belirlenirler. Başlangıç anında, yani $t=0$ iken, bizim kahraman dünya yüzeyinde olacağından \[ r(0) = A = R \] olmalıdır. Bir diğer başlangıç koşulu olarak da kahramanımızın kendisini delikten serbest düşmeye bıraktığını farzedebiliriz. Öyleyse ilk hızı 0 olacaktır. Arkadaşın hız fonksiyonu \[ v(t)=\frac{d r}{dt}=- \omega_0 Rsin(\omega_0 t) + \omega_0 B cos(\omega_0 t)\] olacağı için $t=0$’da iken kahramanın hızının sıfır olması gerektiğinden \[B=0 \] olması gerektiğini buluruz ve problemin çözümü bitmiş olur. Yani bizim deli manyağın Dünya’nın merkezine göre konumu \[ r(t) = R cos(\omega_0 t)\] fonksiyonu ile verilir. Bu da demek oluyor ki bizim kahraman dünyanın bir o yüzeyine bir bu yüzeyine yay gibi gidip gelecek, ölümünü bu delik içinde görecek demektir. Bu salınımın periyoduna da $T$ dersek bu periyot \begin{align}
T =& \frac{2 \pi}{\omega_0 }\\
=& 2 \pi \sqrt{\frac{R^3}{G_N M_\oplus}}
\end{align} olarak hesaplanır.
Bu noktada son olarak gâvurların fun-fact dedikleri birkaç ilginç şeyi hesaplayalım. $G_N$, $M_\oplus$ ve $R$ değerlerini kullanarak kahramanımızın dünyanın diğer ucuna ne kadar sürede ulaşacağını ve tam dünya merkezinden geçer süratinin ne kadar olacağını bulabiliriz. Hareketin periyodunu hesaplarsak yaklaşık $T=5072 s$ olarak bulunur ki bu da yaklaşık 84 dakika 32 saniyeye tekabül eder. Demek ki 42 dakika 16 saniye sonra dünyanın bir ucundan diğer ucuna çıkmak mümkün olur. Bu da epey hızlı bir yolculuk yaptığı anlamına gelir. Kahramanımız tam dünyanın merkezinden geçerken en yüksek sürate sahip olacağından bunun değeri de $v_{max} = \omega_0 R = \sqrt{ \frac{G_N M_\oplus}{R}}$ olarak bulunur. Sayısal değerler yerine yerleştirince $v_{max} = 7903,92\ m/s = 2195\ km/h $ bulunur. Sesin havadaki hızının değeri olan 1235,5 km/h ile kıyaslarsak kahramanımız iyi bir süpersonik uçağın hızıyla Dünya çekirdeğinden geçer.
Ezcümle basit bir fizik eğlencesi böylece sona erdi. Bir diğerinde buluşmak üzere.

